Now AI is collapsing that timeline, stripping away the vessel, and forcing a clearer view of what was actually defensible all along.

If software becomes nearly free to build and AI models become commoditized, where does economic value actually get captured?

Software is no longer a moat

No one can build Chrome in a weekend yet, but the amount of human-years it took to write that code are compressing by Nx or more. AI companies know this, so they’re scrambling to build secondary moats: vertically integrated software platforms on top of their models, and user feedback loops that generate proprietary training data.

Software will probably never be truly “free”, there will always be human product management, design decisions, and coordination involved. But the cost curve is dropping fast enough that software alone can no longer protect a business. The companies that thought they were selling software were often really selling something else. AI makes that distinction impossible to ignore.

Data isn’t the best moat either

As Ilya Sutskever put it: “We’ve achieved peak data and there’ll be no more”, comparing human-generated content to a finite resource like oil.

And even this scarcity might not matter. Synthetic data is proving nearly as good as real data, sometimes better for edge cases. The data moat is eroding faster than most expected.

What moats still exist?

In a world where both AI models and software are commoditized, value gets captured elsewhere

Compute - Physical infrastructure is hard to replicate. In the short run, compute is scarce and the supply chain for creating more is undersupplied. Cloud providers like GCP, Azure, and AWS will have serious moats as long as GPU capacity remains a genuinely scarce resource.

Human relationships - Partnerships, contracts, brand recognition, and social networks are hard to replace even if the underlying software becomes trivial to rebuild.

Capital - Cash in the bank to weather competition and outlast races to the bottom.

Proprietary data - Not scraped or synthesized data, but data that only you can generate: operational data, customer behavior, private records.

Team - Rare talent that competitors can’t easily hire away.

Exclusive rights - Patents, trademarks, copyrights, regulatory licenses.

Network effects - Value that scales with users in ways that are hard to bootstrap from scratch.

The weakest position

Companies with the weakest moats right now are probably pure software companies. SaaS businesses and AI model creators who bet that the software or model itself was the defensible asset. It wasn’t. The question for all of them is: what’s the real moat underneath?

The strongest moats

So what will have the strongest moats in an AI-commoditized world?

Energy and logistics - Companies that can produce and transport energy at scale, with the right land and water rights. AI runs on electricity and cooling; whoever controls those inputs sits at the foundation of the whole stack.

Geography-locked compute - Data centers built next to scarce energy and water sources, where location itself becomes the moat.

Deep relationships - Companies like Meta or ByteDance with billions of users and entrenched network effects. Government contractors locked into long, custom contracts with institutional relationships that take decades to build and are nearly impossible to displace, regardless of what software can do.

The set of things worth building just got a lot bigger. The moats around those things just got a lot smaller.

Let’s start with an analogy

Suppose you are at home and need to send your passbook to the bank. You have to send this by a bad courier service, in fact they always try to inspect and spy on what’s inside every package. So you buy a locker box with two identical keys. You keep one to yourself and send the other one to the bank. You can’t send the key with the package because the courier service will open the locker box and inspect. You can’t send it separately because this bad courier always makes copies of the keys they deliver in hopes of trying them out on future deliveries. So you walk into the bank yourself to deliver the key to the bank. Now you go home and put the passbook inside the locker box and lock it with your identical key and send it via the bad courier. They deliver the box hopelessly without being able to see what’s inside. It was inefficient, you had to visit the bank yourself first. But can we do better?

This time the bank buys a new kind of locker for this purpose. The new locker box has two keys, one for locking the box (public key), another one for unlocking (private key). The key used to lock can’t be used to unlock the box. The key used to unlock can’t be used to lock the box. The bank sends over the locker box to you along with the locking key (public key). As usual the bad courier makes a copy of the key in hopes of future endeavors. Now you put the passbook inside the box and lock it with your locking key (public key). You keep the key and send the box. The courier tries to unlock the box using the key they have copied, but no luck. It can only be unlocked using the unlocking key (private key) only owned by the bank.

The modern Internet is like the bad courier, filled with hackers inspecting unencrypted packets. We need something similar to the second paragraph to secure Internet communication.

The first paragraph is an analogy of symmetric encryption. The second paragraph discusses asymmetric encryption, which is the category public encryption belongs to. But how could we design such a lock digitally?

The underlying mathematics

We can write our encryption function as \(C = E(M)\) where \(M\) is the message we want to encrypt, \(E\) is the function that does the encryption and \(C\) is the encrypted message. Decryption is \(M = D(C)\). Let’s define our functions.

\(e\) and \(d\) are public and private keys respectively. \(n\) is a large number which is a multiple of two large prime numbers. \(\bmod\) means the modulo operation. Most programming languages represent this by % symbol. Given two positive numbers \(a\) and \(n\) result of \(a \bmod n\) is the reminder when \(a\) divides by \(n\). For example \(7 \bmod 3 = 1\) because when \(7\) divides by \(3\) remainder is \(1\). We could write above equations in another way using modular arithmetic syntax.

If \(a \equiv b \pmod{n}\) then \(a\) and \(b\) have a congruence relationship. That means \(a - b\) is divisible by \(n\) and \(a \bmod n\) and \(b \bmod n\) both have the same remainder.

Now we can write the following congruence relation. This relationship must be true for encryption and decryption to work properly. \(D(E(M))\) must always return original \(M\) back.

Now we need to find a relationship between \(e\) and \(d\) such that \(D(E(M))\) holds true. To move forward we need another equation. For that we are going to start with Fermat’s little theorem from number theory. The theorem states the following

If \(p\) is a prime number and \(a\) is any integer, \(a^p - a\) is an integer multiple of \(p\). We can also write this as

Removing \(a\) from both sides we get

Now let’s look at a function called Euler’s totient function. In number theory Euler’s totient function counts the number of positive integers for a given integer \(n\) that are relatively prime to \(n\). Relative primes are numbers that don’t have common divisors other than \(1\). If \(a\) and \(b\) are relatively prime then we can write that the greatest common divisor is \(1\). We usually write this as \(gcd(a, b) = 1\). For example \(10\) and \(7\) are relatively prime because \(gcd(10, 7) = 1\). Now to the totient function, notice that if \(n\) is a prime all the positive integers less than \(n\) are relatively prime to \(n\). We can write this as

So what does it have to do with our previous equations? Now we can write something like this using Euler’s totient function.

Now we are going to prepare the above equations to match \(M^{ed} \equiv M \pmod{n}\) which is similar to \(M \equiv D(E(M)) \equiv (M^e)^d \pmod{n}\) with some reordering. As the first step of the preparation, take the power \(k\) on both sides

Since \(1^k\) is \(1\)

Now Let’s multiply both sides by \(M\)

Now we also have the following equation

Did you notice the similarity in the right side of the two equations? Now we can write

Now this is exactly the following by the definition of modular arithmetic syntax.

We can expand \(\phi(n)\) further because \(n\) is a multiple of two prime numbers.

So we can write

Now choose a random private key \(d\) such that \(1 < d < \phi(n)\) and \(gcd(d, \phi(n)) = 1\) (which means they need to be relatively prime). Now we can find \(e\) using the modular inverse algorithm.

Now that we have found keys \(e\) and \(d\) we can use them to encrypt and decrypt messages. In the next section I will give a numeric example which will clear up most of the details.

Numerical example

Let’s choose two prime numbers \(p\) and \(q\). We choose small values to make calculations easier but in practice the RSA algorithm uses very large prime numbers.

And let’s calculate the Euler’s totient function

Now we choose \(d\) such that it’s relatively prime to \(\phi(n)\). Let’s say

Now compute \(e\) such that

If \(e = 3\) then \(7 \times 3 \bmod 20 = 1\) satisfies the equation.

Now the private key is \(d = (7, 33)\) and the public key is \(e = (3, 33)\). Now let’s encrypt some number \(M = 2\) using the public key. Of course if you need to encrypt characters you must convert them to integers first.

Now let’s decrypt \(C\) using the private key.

It works :). I’ve implemented this as a toy algorithm using python. Never implement your own cryptography algorithms though, for use in production environments.

from __future__ import division
from Crypto.Util import number
import os
from fractions import gcd

from Crypto.Util import number for generating random primes.

class RSA:    
    p = q = n = d = e = pi_n = 0
    
    def __init__(self):        
        self.generate()
        
    def generate(self):        
        self.p = number.getPrime(10, os.urandom)
        self.q = number.getPrime(10, os.urandom)        
        self.n = self.p * self.q        
        self.pi_n = (self.p - 1) * (self.q - 1)        
        self.d = self.choose_d()        
        self.e = self.choose_e()
        
    def choose_d(self):        
        self.d = self.find_a_coprime(self.pi_n)        
        return self.d
                    
    def find_a_coprime(self, a):        
        for i in range(2, a):            
            if gcd(i, a) == 1:                
                return i
            
    def choose_e(self):        
        for i in range(self.n):            
            if (i * self.d) % self.pi_n == 1:                
                return i
    
    def public_key(self):        
        return (self.e, self.n)
    
    def private_key(self):        
        return (self.d, self.n)
    
    def encrypt(self, m, key):        
        return pow(m, key[0]) % key[1]
    
    def decrypt(self, c, key):        
        return pow(c, key[0]) % key[1]

Now we can create RSA class

rsa = RSA()

Following should output 99 if our algorithm works and it does :)

rsa.decrypt(rsa.encrypt(99, rsa.public_key()), rsa.private_key())

How is it secure

The whole security of public key encryption depends on the fact that given a public key no one should be able to generate the private key from that public key. Remember \(ed \equiv 1 \pmod{\phi(n)}\)? So, to calculate d from e an attacker needs to know \(\phi(n)\). But the only way to calculate that is \((p - 1)(q - 1)\). Only the key generator knows \(p\) and \(q\). When \(p\) and \(q\) are large enough no one can calculate (yet!) \(p\) and \(q\) from \(n\). The whole cryptosystem depends on this assumption.

Practical usage

Public key cryptography is used everywhere. HTTPS runs on public key cryptography (not only RSA but it plays a huge role). If you need to use public key cryptography for your own application you can use openssl. openssl is a full featured toolkit which can generate RSA keys among lots of other things. To generate a key pair type the following in the command line (assuming you are on a UNIX based system)

openssl genpkey -algorithm RSA -out private_key.pem -pkeyopt rsa_keygen_bits:2048

You will generate a private_key.pem file from the above command. In this key there is lots of information encoded so that it can be used to extract the public key.

openssl rsa -pubout -in private_key.pem -out public_key.pem

public_key.pem only contains details to encrypt or decrypt something so it can be shared. But you should never share your private_key.pem

Now let’s encrypt some data using public key.

echo "reqviescat in constantia, ergo, repræsentatio cvpidi avctoris religionis" > key.bin

openssl rsautl -encrypt -inkey public_key.pem -pubin -in key.bin -out key.bin.enc

Encrypted data is written to key.bin.enc. Now let’s decrypt it again

openssl rsautl -decrypt -inkey private_key.pem -in key.bin.enc -out key.bin

If you open the key.bin file you can see that the same data is there.

Additional resources

• Toy RSA Algorithm - GitHub
• Original RSA Paper - A Method for Obtaining Digital Signatures and Public-Key Cryptosystems
• Modular Arithmetic - Wikipedia
• Fermat’s Little Theorem - Wikipedia
• Coprime integers - Wikipedia
• Euler’s totient function - Wikipedia
• Modular multiplicative inverse - Wikipedia

Installation

Instructions are for OSX. Steps are as follows

• First install Anaconda.
• Then create python 3 virtual environment with conda create -n py3 python=3.6.
• Then type source activate py3 which will activate python 3 environment.
• Now install opencv with conda install -c conda-forge opencv.
• Check the installation with echo -e "import cv2; print(cv2.__version__)" | python command. It should output 3.3.0
• Make sure your system has ffmpeg installed which is required for reading a video stream from video formats like mp4, mkv. Using brew you can install ffmpeg with one command brew install ffmpeg

Time for action

Let’s do a quick implementation.

import cv2

cap = cv2.VideoCapture("input.mp4")
face_cascade = cv2.CascadeClassifier('haarcascade_frontalface_default.xml')

while(True):
    ret, frame = cap.read()
    gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
    faces = face_cascade.detectMultiScale(gray, 1.3, 5) 
    
    for (x,y,w,h) in faces:
      cv2.rectangle(frame, (x, y), (x+w, y+h), (0 , 0, 255), 2)
    
    cv2.imshow('frame', frame)

    if cv2.waitKey(1) & 0xFF == ord('q'):        
        break

cap.release()
cv2.destroyAllWindows()

We are going to read a video file frame by frame, applying the Viola Jones algorithm with trained parameters then apply a rectangle layer if a face is found, displaying the modified output frame by frame.

cap = cv2.VideoCapture("input.mp4") imports the video. You can also use a web cam instead of video, just pass 0 as parameter like cap = cv2.VideoCapture(0).

Next we are going to load the trained model. haarcascade_frontalface_default.xml is a model already trained using lots of faces and non-faces and lots of computing power. Training good models sometimes takes days not hours. Thankfully the above model is trained by Intel using lots of data. The model we are using here comes with the installation of OpenCV. Generally you can find those models at your opencv-installation-directory/share/OpenCV/haarcascades but this could differ depending on your OS and installation method.

Next in the while loop we are reading frame by frame. Then get the given frame and convert it into grayscale.

gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

A frame is an array of 3 matrices where each matrix is for the respective color blue, green, red. Did you notice the reversed order? In OpenCV the default representation is BGR not RGB. In the above step we are converting it to a grayscale image. gray is a single matrix now.

faces = face_cascade.detectMultiScale(gray, 1.3, 5) 

detectMultiScale function detects faces and returns an array of position coordinates and sizes. The second parameter is scaleFactor. To reduce true negatives you must use a value near to zero. Basically the algorithm can only detect its trained size usually around 20x20 pixels. To detect large objects the area gets scaled by scaleFactor. If scaleFactor is \(1.05\) the scaled block size would equal to \(20 \times 1.05 = 21\). If scaleFactor is equal to 1.3 in the above image the scaled block size is \(20 \times 1.3 = 26\) so you may miss some pixels, and thus some faces. The trade-off is accuracy vs performance.

The 3rd parameter is minNeighbors. It defines how many neighbor rectangles should be identified to retain it. Higher value means fewer false positives.

Next we draw red rectangles if faces are detected. Notice how we passed the red color in BGR format (0 , 0, 255).

for (x,y,w,h) in faces:
      cv2.rectangle(frame, (x, y), (x+w, y+h), (0 , 0, 255), 2)

Next we are writing to a window frame by frame. If you press the key q the loop will break and the video will stop. I’ve created a quick video from the output here. Notice how it detects only frontal faces because the model is trained for frontal faces.

How it works

The Viola Jones algorithm is a machine learning algorithm developed by Paul Viola and Michael Jones in 2001. It was designed to be very fast, even fast enough to be possible in embedded systems. We can break it down into 4 parts

• Haar like features
• Integral image
• AdaBoost (Adaptive Boosting)
• Cascading

Haar like features

Haar-like features, named after the Hungarian mathematician Alfred Haar, are a way of identifying features in an image in a more abstract way.

To calculate a feature following equation is used.

In the case of face detection the following feature will give a higher value in the positioned area, which defines a feature.

Eye areas are generally darker than the area under the eye, so \(\text{(Black area - White area)}\) will give a higher value. And that defines a single feature.

Integral image

Integral image is a way to calculate rectangle features quickly

Every position is the sum of the top and left values. Note this code is written for clarity, there are more efficient ways to write this. In this case you will be feeding a normalized image to the function. The purpose of normalizing first is to get rid of lighting effects.

def my_integral_image(img):
    
    integral_img = np.zeros(img.shape)
    for x in range(img.shape[1]):
        for y in range(img.shape[0]):
            for i in range(x + 1):
                for j in range(y + 1):
                    integral_img[y, x] += img[i, j]
    
    zero_padded_integral_image = np.zeros((img.shape[0] + 1, img.shape[1] + 1))
    
    zero_padded_integral_image[1:img.shape[0] + 1, 1:img.shape[1] + 1] = integral_img
                    
    return zero_padded_integral_image

The whole purpose of integral image is to calculate the sum of pixels inside a given rectangle fast.

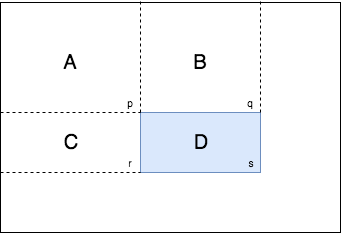
We know values p, q, r, s in the integral image and they represent the sum of all the left and top values. Our goal is to find the pixel sum of D.

So \(D = (p + s) - (q + r)\) which will reduce computation steps to calculate the sum of pixels in the defined rectangle significantly.

Here’s the equivalent python code.

def sum_region(integral_img, top_left, bottom_right):
    # to numpy matrix notation
    top_left = (top_left[1], top_left[0]) 
    bottom_right = (bottom_right[1], bottom_right[0])
    if top_left == bottom_right:
        return integral_img[top_left]
    top_right = (bottom_right[0], top_left[1])
    bottom_left = (top_left[0], bottom_right[1])
    # s + p - (q + r)
    return integral_img[bottom_right] + integral_img[top_left] - integral_img[top_right] - integral_img[bottom_left]    

AdaBoost (Adaptive Boosting)

Now we need a way to select best features from all possible features that can correctly classify a face. AdaBoost algorithm was formulated by Yoav Freund and Robert Schapire in 1997 and won the prestigious Gödel Prize in 2003. This elegant machine learning approach can be applied to wide range of problems not only image detection.

I’ll start with the idea of weak and strong classifiers.

• Weak Classifier - Classifier that’s little bit better than random guessing.
• Strong Classifier - A combination of weak classifiers. It represents wisdom of a weighted crowd of experts.

AdaBoost itself is an inherently incomplete algorithm, so it’s called a meta algorithm. Let’s express the idea of strong classifier mathematically.

H(x) is a strong classifier which classify according to the sign of the sum of weak classifiers. Every weak classifier is a Haar feature combined with some other parameters I’ll detail in the next few paragraphs. Suppose there are only 3 weak classifiers so \(T = 3\). Every classifier outputs +1 or -1 so sum of weak classifier will have either + or - sign.

Here the strong classifier sign is negative so it may not be a face. I started with this analogy but we have to also weight the weak classifiers because some classifiers may have stronger influence than others.

By adding weights the strong classifier gets a little complicated but it’s nothing more than a simple inequality match.

Now how do we decide which weak classifier to use, which \(\alpha\) weights to use? That’s why we need to train over existing labeled data. Suppose image is \(x_i\) and label is \(y_i\) which is 1 for face and 0 for non face. Given example images \((x_1, y_1), ... , (x_m, y_m)\) we will initialize weights for each example. Don’t confuse this weight with the \(\alpha\) weight discussed before. This algorithm has two kind of weights. One is \(\alpha\) weight for selected weak classifier. Other one is for each example and each step denoted by \(w_{t,i}\). Now we are going to intialize weights mentioned later for step one \(t = 1\)

Here we have normalized the weights so the sum of the weights is 1. We do the normalization in every step to make sure the weight distribution always adds up to 1.

The generalized normalized equation is

Next we loop over all the features to select the best weak classifier which minimize error rate.

Here we are calculating the sum of weights of misclassified examples which is the error rate represented by epsilon \(\epsilon\). Notice \(h(x_i, f, p, \theta) - y_i\) returns 1 or -1 if misclassified, 0 if correctly classified. We are taking the absolute value out of it so the weight gets multiplied by 1 if misclassified. Let’s dive into the definition of weak classifier.

\(x_i\) is the \(i\)‘th image example. \(f\) is the Haar feature. \(p\) is the polarity which is either -1 or +1 which defines direction of the inequality. \(\theta\) is the threshold.

To select the \(f\) feature we need to loop over f(x) Haar classifier. To select the threshold we need to minimize the following equation.

Here’s the definition of symbols

• \(T_+\) is total sum of positive sample weights
• \(T_-\) is total sum of negative sample weights
• \(S_+\) is sum of positive sample weights below threshold
• \(S_-\) is sum of negative sample weights below threshold

After finding the minimized error \(\epsilon_t\) for step \(t\) we can find the weights for the next step \(t + 1\)

Where \(e_i = 0\) if sample image \(x_i\) is correctly classified, 1 otherwise. The goal of the equation is to make the weights of incorrectly classified samples slightly larger so in the next round it will be unforgiving to weak classifiers that are going to classify the same samples incorrectly. So in each step it’s going to choose a unique weak classifier with a unique feature. To do so in the above equation correctly classified weights will be decreased so misclassified weights will increase relative to correct weights.

Finally calculate \(\alpha_t\) for the selected classifier.

Notice how \(\alpha\) is going to be a higher value if the error rate is small so that weak classifier has more contribution to the strong classifier.

So finally the algorithm needs to loop \(T\) steps to find \(T\) classifiers to get good results.

Cascading

You may have noticed how many loops we have in the algorithm so this AdaBoost along with Haar Features is computationally expensive for real time detection. So we are using an attentional cascade to reduce some unnecessary computations. A more efficient cascade can be constructed so that negative sub-windows will be rejected early. Every stage of the cascade is a strong classifier, so all the features are grouped into several stages where each stage has several features.

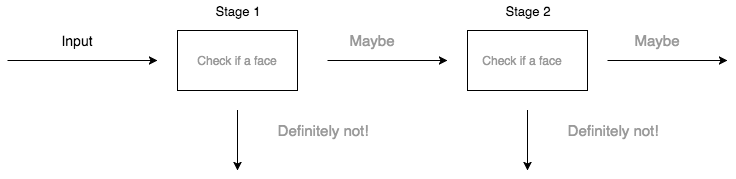
For the cascade we need the following parameters

• Number of stages in cascade
• Number of features in each cascade
• Threshold of each strong classifier

Finding optimum values for above parameters is a difficult task. Viola Jones introduced a simple method to find the optimum combination.

• Select \(f_i\) the maximum acceptable false positive rate per stage
• Select \(d_i\) the maximum acceptable true positive rate per stage
• Select \(F_{target}\) Overall false positive rate

Now we are looping until the predefined \(F_{target}\) is met by adding new stages. In stages we keep adding features until \(f_i\) and \(d_i\) are met. By doing this we are going to create a cascade of strong classifiers.

Additional resources

• Paper (Revised) Viola Jones 2001.
• Viola Jones Python Implementation GitHub
• To learn more about AdaBoost read the book Boosting Foundations and Algorithms. It’s written by the original authors of the algorithm.
• Source code for the face detection in this post - Realtime face detection
• Pull requests are welcome if you find anything wrong in the post - Blog

• Supervised Learning
• Unsupervised Learning

In supervised learning computer learns from input and output while creating a general model which can be used to predict output from new input. Unsupervised learning is about discovering patterns in data without knowing explicit labels beforehand. In this post I’m going to talk about linear regression which is a supervised learning method.

Jupyter Notebook

Jupyter Notebook is an interactive python environment. You can install jupyter notebook with Anaconda which will also install all necessary packages. After installation just run jupyter notebook in command line, which will open jupyter notebook instance in browser. Click New and create a Python 2 notebook.

Enter following lines of code in the cell and press Shift + Enter which will execute the code. Full notebook of the code I used in this post is also available on github.

import numpy as np
import matplotlib.pyplot as plt

Numpy is used for matrix operations. It’s the most important library in python scientific computing ecosystem.

Matplotlib is a plotting library. We will use it to visualize our data.

Data

In this post I’m not going to use any real data set. Instead I’m going to generate some random data.

rng = np.random.RandomState(42)
x = rng.rand(100) * 10
x = x[:, np.newaxis]
b = rng.rand(100) * 5
b = b[:, np.newaxis]
y = 3 * x + b

Here we generate 100 rows of random data we will say \(m = 100\). \(m\) is usually used in machine learning to denote number of data, in this case pairs of \(x\) and \(y\). Now we are going to plot the dataset using Matplotlib.

plt.scatter(x, y)
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.show()

This is the plot generated from the code. Every blue dot is a data point. There are 100 blue dots here.

Data is distributed in a sort of linear nature because of the way we generate random data.

Linear regression

So the purpose of linear regression is to find the equation of a line that does justice to all data points. We will define the equation of the line as \(h(x) = \theta_0 + \theta_1x\). In machine learning \(h(x)\) is called the hypothesis function. But this is just a fancy way of writing old school \(y = mx + c\) where \(c = \theta_0\) and \(m = \theta_1\). Now our goal is to find \(\theta_0\) and \(\theta_1\). If we know the \(\theta_0\) and \(\theta_1\) we can draw the line. To find \(\theta_0\) and \(\theta_1\) we are going to use a function called cost function.

Cost function

We are going to use the following equation which is called the least square method.

The goal is to minimize \((h(x) - y)\) so the difference between the hypothesis function output and \(y\) is minimized as much as possible. Suppose \(\sum_{i=1}^m(h(x^{(i)}) - y^{(i)})^2\) is \(0\), that means \(J(\theta_0, \theta_1) = 0\) so data will fit perfectly to the straight line \(h(x) = \theta_0 + \theta_1x\). But for a real dataset that may not be the case. If data has spread all over the plot this value may be high. Ok, you get now what \((h(x) - y)\) means but why squaring it? We square it because there could be negative or positive values for \(h(x^{(i)}) - y^{(i)}\) depending on the way data is distributed when using a range of values for \(\theta_0\) and \(\theta_1\). By squaring we make sure there are no negative values so there is no cancelling out situations. By that means \(0\) really means that it fits the data distribution. In a real world situation if data is not perfectly linear we can’t get \(J(\theta_0, \theta_1)\) to zero but try to get a minimum value possible. We say this as ‘minimizing the cost function’. We divide by \(m\) to get a relatively small value. We divided by 2 because, by a future derivative operation another function will be a much simpler equation.

Now we are going to implement the cost function in python. First we implement the hypothesis function \(h(x) = \theta_0 + \theta_1x\).

def h(x, theta0, theta1):
    return theta0 + theta1 * x

If we pass normal python integer values to x, theta0, theta1 it will output an integer. What will happen if we change x to a numpy array? All values get multiplied by theta1, then all values will get added by theta0. Output will be a numpy array. This happens because of a python feature called broadcasting. It will save us from writing a for loop to calculate all the values step by step. Broadcasting is a very powerful concept. Use of broadcasting will be used everywhere when doing machine learning in python. Next we implement the cost function in python

def cost(x, theta0, theta1):
    return np.sum(np.power(h(x, theta0, theta1) - y, 2)) * 1 / 2 * x.shape[0]

np.sum() function takes the sum of all the values inside a numpy array and returns a scalar value. np.power() takes power, in this case square of all the values and returns a same size array with modified values. We pass a numpy array as x so x.shape[0] is the number of elements in x which is also equal to \(m\).

Now we need to find theta0 and theta1 which minimize the cost function. One approach is to brute force a range of theta0 and theta1 and pick values where the return value of the cost function is minimal. But can we do better?

Gradient descent

Gradient descent is an iterative algorithm to find out the minimum of a function. This is what we are going to do.

I will explain step by step. First \(:=\) is the assignment operator. In programming languages we use \(=\) operator but in math it means equality. So \(:=\) means assignment in mathematics. \(\alpha\) is called the learning rate which I will explain later in detail. \(\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1)\) is called the derivative part.

This is what the plot looks with \(\theta_0\) against cost function like after 100,000 iterations.

Derivative is measuring the slope, You can see the slope is a negative value as the plot going down. \(\alpha\) is the learning rate which is \(0.0001\). So

You can see \(\theta_0\) will increase because \(\alpha\) is positive and \(\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1)\) is negative. Rate of change in slope is decreasing so \(\theta_0\) will become a stabilized value.

Here’s the derivative steps for \(\theta_0\).

I’ve taken out the \(\frac{1}{2m}\) out of the derivative. Since \(h(x^{(i)}) = \theta_0 + \theta_1x^{(i)}\) we can write

Now we are ready to take the derivative.

Next derivative steps for \(\theta_1\).

After taking the derivative,

Now let’s look at the equivalent python code.

theta0 = 0
theta1 = 0
alpha = 0.001
iteration = 0

while True:    
    temp0 = (1 / m) * np.sum(h(x, theta0, theta1) - y)
    temp1 = (1 / m) * np.sum((h(x, theta0, theta1) - y) * x)
    
    theta0 = theta0 - alpha * temp0
    theta1 = theta1 - alpha * temp1
        
    iteration += 1
    
    if iteration > 100000:
        print("theta0: " + str(theta0) + "theta1:" + str(theta1))
        break

We are initializing theta0 and theta1 to 0. Learning rate alpha to be 0.001. You must choose a smaller value or else it may not converge smoothly. Also note that you must use temporary values while assigning.

Now that we have found optimal theta0 and theta1 values below, we draw a line on top of the first plot.

theta0: 2.567988282theta1:2.98323417806

You can see that the algorithm learned to draw the most optimal line over the data distribution.

Prediction

Here comes the easy part. Now we have a model with learned parameters which can be used to predict. We can use our hypothesis function.

y = h(3, theta1, theta2)

11.517690816184686

Scikit-learn

Scikit Learn is a python library with one of the most used classical machine learning algorithms. Now you know what happens under the hood of the linear regression function. So you are ready to use a library to do production level linear regression machine learning.

Here’s how you import the library

from sklearn.linear_model import LinearRegression

model = LinearRegression()
model.fit(x, y)

fit() function trains the data.

model.predict(3)

11.51769082

You can see that the values are similar to our own implementation.

GitHub repo of example code is available here