Introduction to Machine Learning with Linear Regression
Machine learning is all about computers learning from data to predict new data. There are two types of categories in machine learning
- Supervised Learning
- Unsupervised Learning
In supervised learning computer learns from input and output while creating a general model which can be used to predict output from new input. Unsupervised learning is about discovering patterns in data without knowing explicit labels beforehand. In this post I’m going to talk about linear regression which is a supervised learning method.
Jupyter Notebook
Jupyter Notebook is an interactive python environment. You can install jupyter notebook with Anaconda which will also install all necessary packages. After installation just run jupyter notebook in command line, which will open jupyter notebook instance in browser. Click New and create a Python 2 notebook.
Enter following lines of code in the cell and press Shift + Enter which will execute the code. Full notebook of the code I used in this post is also available on github.
import numpy as np
import matplotlib.pyplot as plt
Numpy is used for matrix operations. It’s the most important library in python scientific computing ecosystem.
Matplotlib is a plotting library. We will use it to visualize our data.
Data
In this post I’m not going to use any real data set. Instead I’m going to generate some random data.
rng = np.random.RandomState(42)
x = rng.rand(100) * 10
x = x[:, np.newaxis]
b = rng.rand(100) * 5
b = b[:, np.newaxis]
y = 3 * x + b
Here we generate 100 rows of random data we will say \(m = 100\). \(m\) is usually used in machine learning to denote number of data, in this case pairs of \(x\) and \(y\). Now we are going to plot the dataset using Matplotlib.
plt.scatter(x, y)
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.show()
This is the plot generated from the code. Every blue dot is a data point. There are 100 blue dots here.
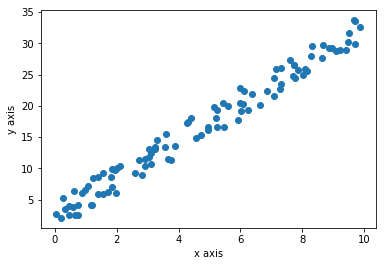
Data is distributed in a sort of linear nature because of the way we generate random data.
Linear Regression
So the purpose of linear regression is to find the equation of a line that does justice to all data points. We will define the equation of the line as \(h(x) = \theta_0 + \theta_1x\). In machine learning \(h(x)\) is called the hypothesis function. But this is just a fancy way of writing old school \(y = mx + c\) where \(c = \theta_0\) and \(m = \theta_1\). Now our goal is to find \(\theta_0\) and \(\theta_1\). If we know the \(\theta_0\) and \(\theta_1\) we can draw the line. To find \(\theta_0\) and \(\theta_1\) we are going to use a function called cost function.
Cost Function
We are going to use the following equation which is called the least square method.
\[J(\theta_0, \theta_1) = \frac{1}{2m}\sum_{i=1}^m(h(x^{(i)}) - y^{(i)})^2\]The goal is to minimize \((h(x) - y)\) so the difference between the hypothesis function output and \(y\) is minimized as much as possible. Suppose \(\sum_{i=1}^m(h(x^{(i)}) - y^{(i)})^2\) is \(0\), that means \(J(\theta_0, \theta_1) = 0\) so data will fit perfectly to the straight line \(h(x) = \theta_0 + \theta_1x\). But for a real dataset that may not be the case. If data has spread all over the plot this value may be high. Ok, you get now what \((h(x) - y)\) means but why squaring it? We square it because there could be negative or positive values for \(h(x^{(i)}) - y^{(i)}\) depending on the way data is distributed when using a range of values for \(\theta_0\) and \(\theta_1\). By squaring we make sure there are no negative values so there is no cancelling out situations. By that means \(0\) really means that it fits the data distribution. In a real world situation if data is not perfectly linear we can’t get \(J(\theta_0, \theta_1)\) to zero but try to get a minimum value possible. We say this as ‘minimizing the cost function’. We divide by \(m\) to get a relatively small value. We divided by 2 because, by a future derivative operation another function will be a much simpler equation.
Now we are going to implement the cost function in python. First we implement the hypothesis function \(h(x) = \theta_0 + \theta_1x\).
def h(x, theta0, theta1):
return theta0 + theta1 * x
If we pass normal python integer values to x, theta0, theta1 it will output an integer. What will happen if we change x to a numpy array? All values get multiplied by theta1, then all values will get added by theta0. Output will be a numpy array. This happens because of a python feature called broadcasting. It will save us from writing a for loop to calculate all the values step by step. Broadcasting is a very powerful concept. Use of broadcasting will be used everywhere when doing machine learning in python. Next we implement the cost function in python
def cost(x, theta0, theta1):
return np.sum(np.power(h(x, theta0, theta1) - y, 2)) * 1 / 2 * x.shape[0]
np.sum() function takes the sum of all the values inside a numpy array and returns a scalar value. np.power() takes power, in this case square of all the values and returns a same size array with modified values. We pass a numpy array as x so x.shape[0] is the number of elements in x which is also equal to \(m\).
Now we need to find theta0 and theta1 which minimize the cost function. One approach is to brute force a range of theta0 and theta1 and pick values where the return value of the cost function is minimal. But can we do better?
Gradient Descent
Gradient descent is an iterative algorithm to find out the minimum of a function. This is what we are going to do.
\[\theta_0 := \theta_0 - \alpha \frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1)\] \[\theta_1 := \theta_1 - \alpha \frac{\partial}{\partial \theta_1} J(\theta_0, \theta_1)\]I will explain step by step. First \(:=\) is the assignment operator. In programming languages we use \(=\) operator but in math it means equality. So \(:=\) means assignment in mathematics. \(\alpha\) is called the learning rate which I will explain later in detail. \(\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1)\) is called the derivative part.
\[\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) = \frac{\partial}{\partial \theta_0} \frac{1}{2m}\sum_{i=1}^m(h(x^{(i)}) - y^{(i)})^2\]This is what the plot looks with \(\theta_0\) against cost function like after 100,000 iterations.
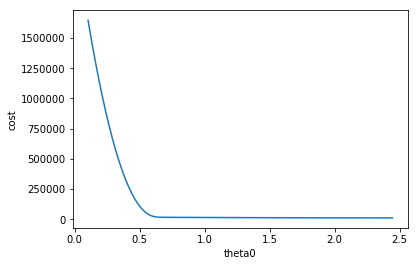
Derivative is measuring the slope, You can see the slope is a negative value as the plot going down. \(\alpha\) is the learning rate which is \(0.0001\). So
\[\theta_0 := \theta_0 - \alpha \frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1)\]You can see \(\theta_0\) will increase because \(\alpha\) is positive and \(\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1)\) is negative. Rate of change in slope is decreasing so \(\theta_0\) will become a stabilized value.
Here’s the derivative steps for \(\theta_0\).
\[\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) = \frac{1}{2m} \frac{\partial}{\partial \theta_0} \sum_{i=1}^m(h(x^{(i)}) - y^{(i)})^2\]I’ve taken out the \(\frac{1}{2m}\) out of the derivative. Since \(h(x^{(i)}) = \theta_0 + \theta_1x^{(i)}\) we can write
\[\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) = \frac{1}{2m} \frac{\partial}{\partial \theta_0} \sum_{i=1}^m(\theta_0 + \theta_1x^{(i)} - y^{(i)})^2\]Now we are ready to take the derivative.
\[\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=1}^m(\theta_0 + \theta_1x^{(i)} - y^{(i)})\]Next derivative steps for \(\theta_1\).
\[\frac{\partial}{\partial \theta_1} J(\theta_0, \theta_1) = \frac{1}{2m} \frac{\partial}{\partial \theta_1} \sum_{i=1}^m(h(x^{(i)}) - y^{(i)})^2\] \[\frac{\partial}{\partial \theta_1} J(\theta_0, \theta_1) = \frac{1}{2m} \frac{\partial}{\partial \theta_1} \sum_{i=1}^m(\theta_0 + \theta_1x^{(i)} - y^{(i)})^2\]After taking the derivative,
\[\frac{\partial}{\partial \theta_1} J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=1}^m(\theta_0 + \theta_1x^{(i)} - y^{(i)})x^{(i)}\]Now let’s look at the equivalent python code.
theta0 = 0
theta1 = 0
alpha = 0.001
iteration = 0
while True:
temp0 = (1 / m) * np.sum(h(x, theta0, theta1) - y)
temp1 = (1 / m) * np.sum((h(x, theta0, theta1) - y) * x)
theta0 = theta0 - alpha * temp0
theta1 = theta1 - alpha * temp1
iteration += 1
if iteration > 100000:
print("theta0: " + str(theta0) + "theta1:" + str(theta1))
break
We are initializing theta0 and theta1 to 0. Learning rate alpha to be 0.001. You must choose a smaller value or else it may not converge smoothly. Also note that you must use temporary values while assigning.
Now that we have found optimal theta0 and theta1 values below, we draw a line on top of the first plot.
theta0: 2.567988282theta1:2.98323417806
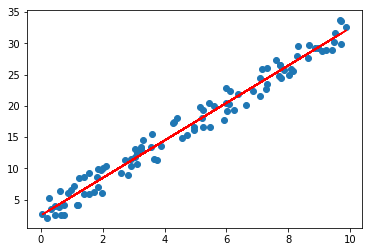
You can see that the algorithm learned to draw the most optimal line over the data distribution.
Prediction
Here comes the easy part. Now we have a model with learned parameters which can be used to predict. We can use our hypothesis function.
y = h(3, theta1, theta2)
11.517690816184686
Scikit Learn
Scikit Learn is a python library with one of the most used classical machine learning algorithms. Now you know what happens under the hood of the linear regression function. So you are ready to use a library to do production level linear regression machine learning.
Here’s how you import the library
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x, y)
fit() function trains the data.
model.predict(3)
11.51769082
You can see that the values are similar to our own implementation.
GitHub repo of example code is available here