Detection is an important application of computer vision. In this post I’m going to detail how to do real time face detection using the Viola Jones Algorithm introduced in the paper Rapid object detection using a boosted cascade of simple features (2001). Mind the word detection, we are not going to recognize, meaning which one the face belongs to. This is merely detection that there is a face in a given image. We are going to use OpenCV (Open Source Computer Vision Library). OpenCV is written in C++ but there are interfaces for other languages so we will use, preferably python.

Installation

Instructions are for OSX. Steps are as follows

  • First install Anaconda.
  • Then create python 3 virtual environment with conda create -n py3 python=3.6.
  • Then type source activate py3 which will activate python 3 environment.
  • Now install opencv with conda install -c conda-forge opencv.
  • Check the installation with echo -e "import cv2; print(cv2.__version__)" | python command. It should output 3.3.0
  • Make sure your system has ffmpeg installed which is required for reading a video stream from video formats like mp4, mkv. Using brew you can install ffmpeg with one command brew install ffmpeg

Time for action

Let’s do a quick implementation.

import cv2

cap = cv2.VideoCapture("input.mp4")
face_cascade = cv2.CascadeClassifier('haarcascade_frontalface_default.xml')

while(True):
    ret, frame = cap.read()
    gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
    faces = face_cascade.detectMultiScale(gray, 1.3, 5) 
    
    for (x,y,w,h) in faces:
      cv2.rectangle(frame, (x, y), (x+w, y+h), (0 , 0, 255), 2)
    
    cv2.imshow('frame', frame)

    if cv2.waitKey(1) & 0xFF == ord('q'):        
        break

cap.release()
cv2.destroyAllWindows()

We are going to read a video file frame by frame, applying the Viola Jones algorithm with trained parameters then apply a rectangle layer if a face is found, displaying the modified output frame by frame.

cap = cv2.VideoCapture("input.mp4") imports the video. You can also use a web cam instead of video, just pass 0 as parameter like cap = cv2.VideoCapture(0).

Next we are going to load the trained model. haarcascade_frontalface_default.xml is a model already trained using lots of faces and non-faces and lots of computing power. Training good models sometimes takes days not hours. Thankfully the above model is trained by Intel using lots of data. The model we are using here comes with the installation of OpenCV. Generally you can find those models at your opencv-installation-directory/share/OpenCV/haarcascades but this could differ depending on your OS and installation method.

Next in the while loop we are reading frame by frame. Then get the given frame and convert it into grayscale.

gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

A frame is an array of 3 matrices where each matrix is for the respective color blue, green, red. Did you notice the reversed order? In OpenCV the default representation is BGR not RGB. In the above step we are converting it to a grayscale image. gray is a single matrix now.

faces = face_cascade.detectMultiScale(gray, 1.3, 5)

detectMultiScale function detects faces and returns an array of position coordinates and sizes. The second parameter is scaleFactor. To reduce true negatives you must use a value near to zero. Basically the algorithm can only detect its trained size usually around 20x20 pixels. To detect large objects the area gets scaled by scaleFactor. If scaleFactor is \(1.05\) the scaled block size would equal to \(20 \times 1.05 = 21\). If scaleFactor is equal to 1.3 in the above image the scaled block size is \(20 \times 1.3 = 26\) so you may miss some pixels, and thus some faces. The trade-off is accuracy vs performance.

The 3rd parameter is minNeighbors. It defines how many neighbor rectangles should be identified to retain it. Higher value means fewer false positives.

Next we draw red rectangles if faces are detected. Notice how we passed the red color in BGR format (0 , 0, 255).

for (x,y,w,h) in faces:
      cv2.rectangle(frame, (x, y), (x+w, y+h), (0 , 0, 255), 2)

Next we are writing to a window frame by frame. If you press the key q the loop will break and the video will stop. I’ve created a quick video from the output here. Notice how it detects only frontal faces, because the model is trained for frontal faces.

How it works

The Viola Jones algorithm is a machine learning algorithm developed by Paul Viola and Michael Jones in 2001. It was designed to be very fast, even fast enough to be possible in embedded systems. We can break it down into 4 parts

  • Haar like features
  • Integral image
  • AdaBoost (Adaptive Boosting)
  • Cascading

Haar like features

Haar-like features, named after the Hungarian mathematician Alfred Haar, are a way of identifying features in an image in a more abstract way.

Haar

To calculate a feature following equation is used.

\[Value = \text{(Sum of pixels in black area)} - \text{(Sum of pixels in white area)}\]

In the case of face detection the following feature will give a higher value in the positioned area, which defines a feature.

Face

Eye areas are generally darker than the area under the eye, so \(\text{(Black area - White area)}\) will give a higher value. And that defines a single feature.

Integral Image

Integral image is a way to calculate rectangle features quickly

\[ii(x, y) = \sum_{x{'} \le x, y{'} \le y} i(x', y')\]

Every position is the sum of the top and left values. Note this code is written for clarity, there are more efficient ways to write this. In this case you will be feeding a normalized image to the function. The purpose of normalizing first is to get rid of lighting effects.

def my_integral_image(img):
    
    integral_img = np.zeros(img.shape)
    for x in range(img.shape[1]):
        for y in range(img.shape[0]):
            for i in range(x + 1):
                for j in range(y + 1):
                    integral_img[y, x] += img[i, j]
    
    zero_padded_integral_image = np.zeros((img.shape[0] + 1, img.shape[1] + 1))
    
    zero_padded_integral_image[1:img.shape[0] + 1, 1:img.shape[1] + 1] = integral_img
                    
    return zero_padded_integral_image

The whole purpose of integral image is to calculate the sum of pixels inside a given rectangle fast.

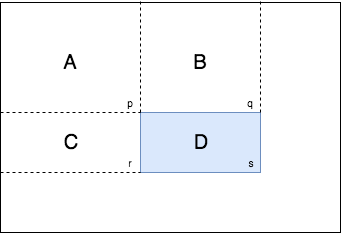
Integral sum

We know values p, q, r, s in the integral image and they represent the sum of all the left and top values. Our goal is to find the pixel sum of D.

\[p = A \\ q = A + B \\ r = A + C \\ s = A + B + C + D \\\]

So \(D = (p + s) - (q + r)\) which will reduce computation steps to calculate the sum of pixels in the defined rectangle significantly.

Here’s the equivalent python code.

def sum_region(integral_img, top_left, bottom_right):
    # to numpy matrix notation
    top_left = (top_left[1], top_left[0]) 
    bottom_right = (bottom_right[1], bottom_right[0])
    if top_left == bottom_right:
        return integral_img[top_left]
    top_right = (bottom_right[0], top_left[1])
    bottom_left = (top_left[0], bottom_right[1])
    # s + p - (q + r)
    return integral_img[bottom_right] + integral_img[top_left] - integral_img[top_right] - integral_img[bottom_left]

AdaBoost (Adaptive Boosting)

Now we need a way to select best features from all possible features that can correctly classify a face. AdaBoost algorithm was formulated by Yoav Freund and Robert Schapire in 1997 and won the prestigious Gödel Prize in 2003. This elegant machine learning approach can be applied to wide range of problems not only image detection.

I’ll start with the idea of weak and strong classifiers.

  • Weak Classifier - Classifier that’s little bit better than random guessing.
  • Strong Classifier - A combination of weak classifiers. It represents wisdom of a weighted crowd of experts.

AdaBoost itself is an inherently incomplete algorithm, so it’s called a meta algorithm. Let’s express the idea of strong classifier mathematically.

\[H(x) = sign\Big( h_1(x) + h_2(x) + ... +h_T(x)\Big)\]

H(x) is a strong classifier which classify according to the sign of the sum of weak classifiers. Every weak classifier is a Haar feature combined with some other parameters I’ll detail in the next few paragraphs. Suppose there are only 3 weak classifiers so \(T = 3\). Every classifier outputs +1 or -1 so sum of weak classifier will have either + or - sign.

\[H(x) = sign\Big( +1 + -1 + -1 \Big)\]

Here the strong classifier sign is negative so it may not be a face. I started with this analogy but we have to also weight the weak classifiers because some classifiers may have stronger influence than others.

By adding weights the strong classifier gets a little complicated but it’s nothing more than a simple inequality match.

\[H(x) = \begin{cases} +1, \text{if}\ \sum_{t = 1}^{T} \alpha_th_t(x) \ge \frac{1}{2} \sum_{t = 1}^{T} \alpha_t \\ -1, \text{otherwise} \end{cases}\]

Now how do we decide which weak classifier to use, which \(\alpha\) weights to use? That’s why we need to train over existing labeled data. Suppose image is \(x_i\) and label is \(y_i\) which is 1 for face and 0 for non face. Given example images \((x_1, y_1), ... , (x_m, y_m)\) we will initialize weights for each example. Don’t confuse this weight with the \(\alpha\) weight discussed before. This algorithm has two kind of weights. One is \(\alpha\) weight for selected weak classifier. Other one is for each example and each step denoted by \(w_{t,i}\). Now we are going to intialize weights mentioned later for step one \(t = 1\)

\[w_{1, i} = \frac{1}{m}\]

Here we have normalized the weights so the sum of the weights is 1. We do the normalization in every step to make sure the weight distribution always adds up to 1.

\[\sum_{i = 1}^{m} w_{t, i} = 1\]

The generalized normalized equation is

\[w_{t,i} = \frac{w_{t,i}}{\sum_{j = 0}^{m}w_{t,i}}\]

Next we loop over all the features to select the best weak classifier which minimize error rate.

\[\epsilon_t = min_{f, p, \theta} \sum_{i = 1}^m w_{t, i} | h(x_i, f, p, \theta) - y_i |\]

Here we are calculating the sum of weights of misclassified examples which is the error rate represented by epsilon \(\epsilon\). Notice \(h(x_i, f, p, \theta) - y_i\) returns 1 or -1 if misclassified, 0 if correctly classified. We are taking the absolute value out of it so the weight gets multiplied by 1 if misclassified. Let’s dive into the definition of weak classifier.

\[h(x) = h(x_i, f, p, \theta)\]

\(x_i\) is the \(i\)‘th image example. \(f\) is the Haar feature. \(p\) is the polarity which is either -1 or +1 which defines direction of the inequality. \(\theta\) is the threshold.

\[h(x, f, p , \theta) = \begin{cases} 1, \text{if } pf(x) \lt p\theta \\ 0, \text{otherwise} \end{cases}\]

To select the \(f\) feature we need to loop over f(x) Haar classifier. To select the threshold we need to minimize the following equation.

\[error_{\theta} = min\Big( (S_+) + (T_-) - (S_-), (S_-) + (T_+) - (S_+))\Big)\]

Here’s the definition of symbols

  • \(T_+\) is total sum of positive sample weights
  • \(T_-\) is total sum of negative sample weights
  • \(S_+\) is sum of positive sample weights below threshold
  • \(S_-\) is sum of negative sample weights below threshold

After finding the minimized error \(\epsilon_t\) for step \(t\) we can find the weights for the next step \(t + 1\)

\[w_{t+1, i} = w_{t, i} \Big(\frac{\epsilon_t}{1 - \epsilon_t}\Big)^{1 -e_i}\]

Where \(e_i = 0\) if sample image \(x_i\) is correctly classified, 1 otherwise. The goal of the equation is to make the weights of incorrectly classified samples slightly larger so in the next round it will be unforgiving to weak classifiers that are going to classify the same samples incorrectly. So in each step it’s going to choose a unique weak classifier with a unique feature. To do so in the above equation correctly classified weights will be decreased so misclassified weights will increase relative to correct weights.

Finally calculate \(\alpha_t\) for the selected classifier.

\[\alpha_t = log(\frac{1 - \epsilon_t}{\epsilon_t})\]

Notice how \(\alpha\) is going to be a higher value if the error rate is small so that weak classifier has more contribution to the strong classifier.

So finally the algorithm needs to loop \(T\) steps to find \(T\) classifiers to get good results.

Cascading

You may have noticed how many loops we have in the algorithm so this AdaBoost along with Haar Features is computationally expensive for real time detection. So we are using an attentional cascade to reduce some unnecessary computations. A more efficient cascade can be constructed so that negative sub-windows will be rejected early. Every stage of the cascade is a strong classifier, so all the features are grouped into several stages where each stage has several features.

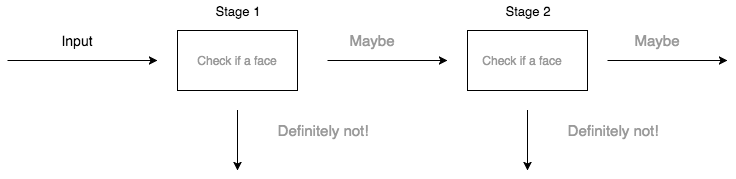
Cascade

For the cascade we need the following parameters

  • Number of stages in cascade
  • Number of features in each cascade
  • Threshold of each strong classifier

Finding optimum values for above parameters is a difficult task. Viola Jones introduced a simple method to find the optimum combination.

  • Select \(f_i\) the maximum acceptable false positive rate per stage
  • Select \(d_i\) the maximum acceptable true positive rate per stage
  • Select \(F_{target}\) Overall false positive rate

Now we are looping until the predefined \(F_{target}\) is met by adding new stages. In stages we keep adding features until \(f_i\) and \(d_i\) are met. By doing this we are going to create a cascade of strong classifiers.

Additional Resources